NOTE: This post implements a rather convoluted and poorly optimized version of the Dijkstra’s algorithm; so for now I’d recommend using another source. I’ll update the post with a better implementation soon.

Happy new year! It’s been a while since I wrote anything here, and I thought it was about time I did so. This time, I’ll talk about this really popular, really important, and really cool algorithm.

One 1956 morning in Amsterdam, a 26-year old Edsger Wybe Dijkstra was shopping with his fiancée. Tired, he sat down on a café terrace to drink a coffee, and that’s when it happened. In twenty minutes, he designed an algorithm that today is one of the most important ones today, used everywhere from Google Maps to network packet routing. It is the eponymous Dijkstra’s algorithm, used to find the shortest path between nodes in a graph.

Today, I spent pretty much my entire afternoon trying to understand and implement it. It was a pretty hard time, but I think I now understand it to a good enough extent to be able to explain it to y’all here. So here I go.

Background

As I stated earlier, Dijkstra’s algorithm is an algorithm used to find the shortest path between graph nodes. Specifically, the graph must be a weighted one and every weight must be non-negative. This is important, as negative weights will entirely mess up the algorithm’s calculations. There’s a different algorithm called the Bellman-Ford algorithm for that purpose. The graph may be either directed or undirected.

The Algorithm

Let’s take this graph:

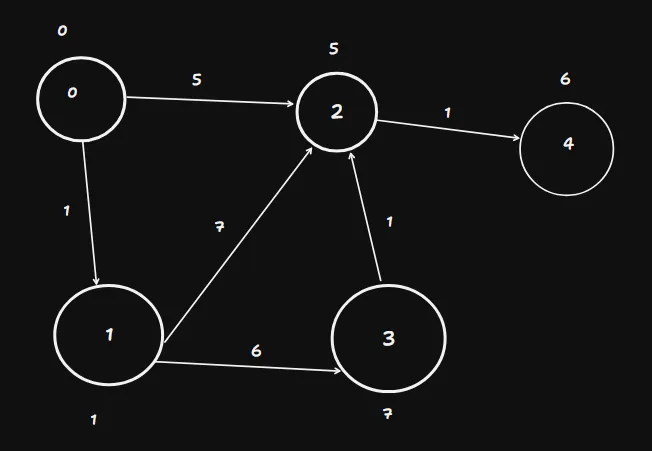
Someone asks you, “Hey, what’s the shortest path between 0 and 4?” You can just take a look at the graph and quickly notice, it’s 0-2-4 among the three possible paths. Let’s see how Dijkstra’s algorithm helps a computer do this act of noticing.

Step 1: Prepping for the journey

Create a set of all the unvisited notes, and we’ll call it, as expected, the unvisited set. The data structure to use for this purpose is a priority queue. Don’t worry if that sounds difficult, you can also just use a normal list and manage the priority thing yourself, I’ll tell you how later on.

List<DijkstraNode> unvisited = [];

You’ll also create a map called predecessor. This will be important near the end when we construct the shortest path. Basically, each key in this map represents a graph node index and each value represents that node’s predecessor node.

Map<int, int?> predecessor = {};

Another list we’ll create is this:

List<DijkstraNode> visited = [];

This is something we’ll fill with the nodes we visit as we go through the algorithm.

Also, just for reference, here is the definition for the class DijkstraNode:

class DijkstraNode {
  GraphNode node;
  int nodeIdx;
  int distance;

  DijkstraNode(this.node, this.nodeIdx, this.distance);

  @override
  String toString() {
    var sb = StringBuffer();
    sb.write("{");
    sb.write("idx: $nodeIdx, dist: $distance");
    sb.write("}");
    return sb.toString();
  }
}

It simply holds the node object itself, the index to it, and distance which is something I’ll explain in step 2. Alongside those, it has a constructor and a convenient stringification function.

Step 2: Initialization

Now, what you’ll do is initialize both unvisited and predecessor.

In this algorithm, we assign each node a distance. This is simply the distance from the source that we have chosen. We start with infinite (or in the case of this program, very high) initial distances for all nodes; that basically says, “We don’t know the distance yet”, and improve these distances as we go on. The exception is the source node, which always has a distance of 0 for obvious reasons.

Additionally, to begin with, we set each predecessor as null.

for (int i = 0; i < nodes.length; i++) {
  var distance = i == 0
      ? 0
      : 9999999; 
  var uv = DijkstraNode(nodes[i], i, distance);
  unvisited.add(uv);
  predecessor[i] = null;
}

Step 3: Journey begins

We’ll now start visiting nodes. We select the current node from the unvisited set, that is, the node with the smallest distance (that’s of course, not infinite).

That is the reason why priority queues with the smallest value first are used here, since the nodes with smaller values get a higher priority.

To begin with, the current node will simply be the source node.

while (!unvisited.isEmpty) {
  var currentNode = unvisited.removeAt(0);
  visited.add(currentNode);

  // ...
}

Note that we’ve begun a loop. This loop will run as long as there’s a node we haven’t visited. As soon as we’ve visited everything, the loop ends.

Also note that we’re removing the current node from the unvisited array. Of course, that’s because since we’re visiting it now, it’s no longer unvisited. We’ll proceed to add it to the visited list.

One other way the algorithm could terminate would be when I visit the final node. Now, inherently Dijkstra’s is an algorithm which finds the shortest distance to all nodes from a single one, but if we want to find the distance to just one node, we can just end it here.

while (!unvisited.isEmpty) {
  var currentNode = unvisited.removeAt(0);
  visited.add(currentNode);

  if (currentNode.nodeIdx == end) {
      break;
  }

  // ...
}

In the case of the above graph, node 0 would be the first currentNode.

Step 5: Hello, Neighbor

The next step is to check out all of the unvisited neighbors of the current node. We’ll calculate the distance to them, by adding the distance of the current node with the weight of the edge that points to the neighbor. Then, we’ll check if that value is less than the current distance of the neighbor.

If it is indeed less, we update the distance to that newly calculated value. This is a process known as relaxation.

Sounded like a jumble of words? Okay, so here’s a portion of the above graph, consisting only of the connection between nodes 0 and 1 to demonstrate:

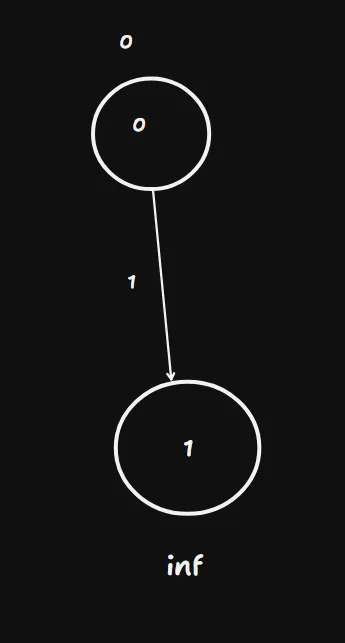
1 has a distance of infinity because it’s set that way to begin with, and node 0 has one of 0 since it’s the source. Now, if the function d(x) gives the distance of a node x and u(x, y) gives the weight of the edge connecting x and y, then we can apply this:

if d(0) + u(0, 1) < d(1)
    d(1) = d(0) + u(0, 1)

As we can see above, d(0) is zero, u(0, 1) is 1 and d(1) is infinity. Hence the if condition is satisfied, and d(1) now becomes 1. Node 1 has been relaxed.

You use this bit of code to implement this:

while (!unvisited.isEmpty) {
  // ...
  if (currentNode.nodeIdx == end) {
      break;
  }

  var node = currentNode.node;
  for (var edge in node.edges) {
    // Grab the index of the edge
    var neighborIndex = unvisited.indexWhere((uv) => uv.nodeIdx == edge.to);
    if (neighborIndex == -1) continue; // Already visited
    var neighborNode = unvisited[neighborIndex];

    // Actual relaxation logic
    if (currentNode.distance + edge.weight < neighborNode.distance) {
      neighborNode.distance = currentNode.distance + edge.weight;
      predecessor[neighborNode.nodeIdx] = currentNode.nodeIdx;
    }
  }

  // ...
}

This process of relaxation will repeat for every neighbor of the current node till they’re all relaxed.

You might have also noticed this little line there in the relaxation logic:

predecessor[neighborNode.nodeIdx] = currentNode.nodeIdx;

We set the predecessor of a relaxed neighbor to be the current node. We’ll be using these values near the end of the algorithm to construct the path to follow.

Fixing our unvisited list

As I said before, the unvisitied list is a priority queue, where the values with smaller distances get a higher priority. However, after a relaxation, the order of the elements in this queue of ours, which is just a normal list, by the way, will be all messed up. We need to fix that.

For this, we just sort in ascending order of distance.

while (!unvisited.isEmpty) {
  // ...
      predecessor[neighborNode.nodeIdx] = currentNode.nodeIdx;
    }
  }

  unvisited.sort((a, b) => a.distance.compareTo(b.distance));
}

If you’re already using a properly implemented priority queue data structure for unvisited, there’s no need to do this since the implementation of that data structure will handle this issue itself.

Now, the process will repeat from step 3, visiting each node in the graph and relaxing neighbors. This will continue till all the nodes are relaxed or in this case, until everything leading upto our target node is relaxed. After that, we’ll end up with all of the distance values updated to reflect the shortest possible distances of each node from the source. These nodes will stay in the visited array.

If we were doing Discrete Math homework, we could just call it quits here. But we’re not done yet. We already know where to find the length of the shortest path; it’s the value of distance on our target node in visited. However, how do we find out the path to take to get there?

This is where the predecessor map we’ve looked at a couple of times comes in.

Step 6: Reconstructing the road

We first create a list to store the path:

List<int> path = [];

It’s a list of ints, because each node’s name is itself an int.

What we’re basically going to do is begin from the last node, then look at its predecessor in the predecessor map. Then we’ll look at that predecessor and so on, and if a path exists between the source and target nodes, we will have backtracked our way through the shortest path. And during this backtracking process, we’ll leave each node we backtracked through in the path list.

So, to backtrack, we first define this:

int? current = end;

This is a nullable integer, that is essentially our index in a sense to backtrack using. Now, we do it.

while (current != null) {
  path.insert(0, current);
  current = predecessor[current];
}

While going through the predecessors, we insert each node through the beginning (as we’re going back, not forward) and keep doing this till we reach the predecessor of the source node 0 itself, which is of course, null. It’s kind of like traversing a doubly linked list from its tail to its head.

Now, this doesn’t always succeed. If there’s no path that exists between the source and target nodes, the path list will be all messed up. So, we have to check for that as well.

if (path.first != start) {
  throw StateError("No path exists from $start to $end.");
}

We now grab the length of the shortest path from the visited array. It’ll just be the distance field of the node whose nodeIdx equals to the index of the target node.

var pathLength = visited.singleWhere((v) => v.nodeIdx == end).distance;

Finally, we’re done; we can now return the results. I defined my Dijkstra function as one that returns a tuple of the path and its length, so I just return this:

return (path, pathLength);

And that’s it.

Quite an incredible algorithm, I have to say. If you want to check out my implementation a bit better, you can take a look at this link.